Sharding as Parallelism

Motivation: We propose a scaling solution for Ethereum’s Layer-2 ecosystem that’s predicated on sharding, specifically zkSharding. While sharding is a promising solution for the scalability problem, its implementation in decentralized networks introduces complexities that aren't present in traditional blockchains nor traditional database sharding. By examining blockchain sharding through the lens of established parallel computing models, we can better understand its potential and limitations.

Why Parallelism?

Let's look at the world's most scalable systems: they are built on interconnected, parallel-working clusters. These systems are exponentially more productive than any single computer. Additionally, their power can be scaled up at will, something that is not possible with a single machine. This capability is possible to parallel execution across thousands of clusters.

A similar idea can be applied to modern decentralized networks in general and blockchains in particular. We are witnessing a renaissance of multi-chain systems in both the Ethereum ecosystem—with 100+ rollups—and the broader decentralized industry.

However, in most multi-chain systems the lack of state access between chains inhibits the ability for application developers to make use of parallel execution.

At =nil; Foundation, we believe that parallel execution is the next step in the industry's evolution and we are confident this can be achieved through blockchain sharding.

Redefining Sharding

First of all, we need to clearly define sharding and delineate between various differences in definitions.

Database sharding, a long-established practice, splits data across multiple storage units to improve access, speed, and security. While database sharding deals with data storage scaling, it does not explicitly define how execution is handled.

At a conceptual level, blochchain sharding can be understood as a collection of decentralized networks (shards), each with its own blockchain, running in parallel. This means that, at any given moment, multiple validators are performing useful work simultaneously. The usefulness of this approach lies in its ability to distribute workloads across multiple processing units (i.e. shards), making the system more efficient and scalable.

Unlike database sharding, blockchain sharding does define how execution is handled; workloads are distributed across multiple processing units (i.e. shards). This seemingly subtle difference makes a significant impact on how we model blockchain sharding. In the following sections we will map concepts of parallel computations to blockchain sharding to reason about its potential and limitations.

Sharding Classification Within the Domain

Every concept that is mapped to another area must be classified within the target domain. Here we're mapping the Parallel Computation Theory or classical parallel execution models to blockchain sharding.

Flynn’s Taxonomy: 
SISD (Single Instruction, Single Data): This is the traditional sequential model, not parallel. 
SIMD (Single Instruction, Multiple Data): One instruction is executed on multiple data points simultaneously. This is common in vector processors and GPUs.
MISD (Multiple Instruction, Single Data): Multiple instructions operate on the same data simultaneously. This is rare in practice.
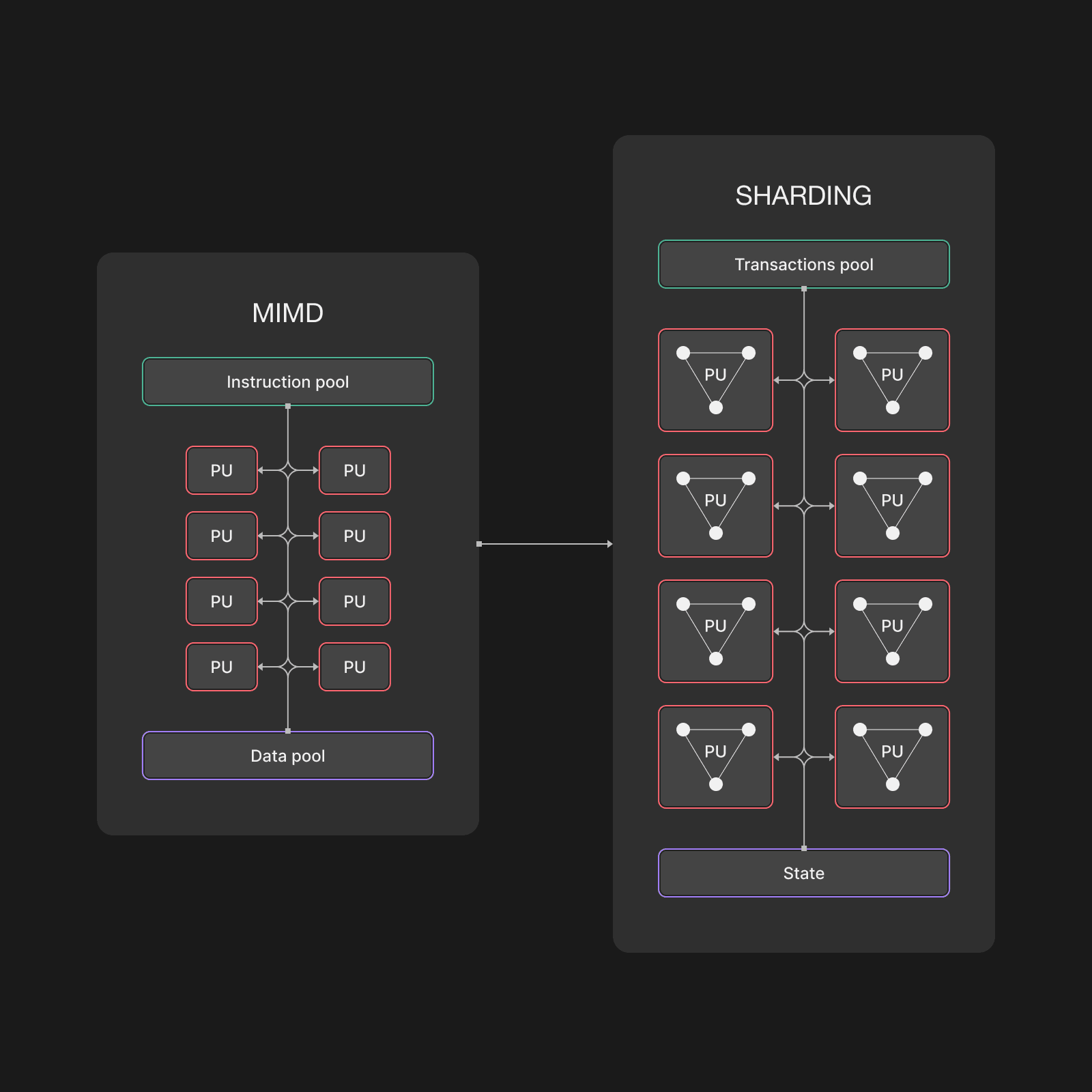
MIMD (Multiple Instruction, Multiple Data): Multiple processors execute different instructions on different data simultaneously. This is the most flexible and common form of parallel computing.

In this classification, blockchain sharding can be understood as the classic MIMD (Multiple Instruction, Multiple Data) model from Flynn's taxonomy. In this context:

1. Each shard functions as a processing unit;
2. The transaction pool serves as the instruction pool;
3. The blockchain's global state represents the shared data.

From this definition, it is clear that each validator operates on different data at any given moment. Since sharding involves no shared data among these segments, it can be classified as a pure form of MIMD. At any point in time, each shard processes its own distinct, non-shared data (see Figure 1).

 

This intuitive classification provides a foundation to demonstrate how a sharded network can support the implementation of an arbitrary set of algorithms with quite strong memory guarantees. Below, we discuss what types of algorithms get the most benefit from such systems.

Application of Computation Models to Decentralized Networks

Applying parallel computation models to decentralized networks provides valuable insights into design limitations and opportunities. This approach allows us to leverage well-established solutions from the parallel computation theory of research to enhance blockchain scalability and performance.

The sharding paradigm defined above can be considered a Parallel Random-Access Machine. More precisely, it functions as a PRAM that utilizes the CREW (Concurrent Read, Exclusive Write) strategy to solve read/write conflicts. The core idea is that while any unit can access memory, it cannot retrieve intermediate values before block propagation and write to it (no concurrent write). Specifically, sharding as a parallel model supports the implementation of CREW algorithms in a sequentially consistent environment.

Establishing this limitation is crucial because, in developing any parallel algorithm, understanding the constraints of the underlying infrastructure is essential. For example, the classic Gaussian elimination algorithm can be efficiently implemented in a CREW model. Another pertinent example in decentralized systems is the All Pairs Shortest Paths algorithm, which is based on Repeated Dijkstra and can be adapted for such models. It is proven that in the CREW case it can be implemented with isoefficiency $\theta(p^3)$, which can be used for making a decision in favor of implementing it in a sharded decentralized network.

Another application is Amdahl's Law, which provides insights into the limitations of sharding. For Amdahl's Law, security, communication, and other factors can be considered the sequential parts of each task, thereby limiting the overall parallelism achievable. That can be applied to understand the efficiency of sharding and proper job fractioning (transaction distribution) across shards.

It's also worth noting that individual processing units, or shards, can be further parallelized. This concept is analogous to Instruction-Level Parallelism (ILP) in traditional CPU architectures. In the context of decentralized networks, this parallelization is referred to as VM parallelization, offering another layer of performance optimization.

Rollups Sharding Explained (setup)

We define sharding in the context of rollups to formally assess its practical application in real-world scenarios.

First, we need to formally define sharding and elaborate on its various aspects.

We begin with the definition of the global data log (blocks) as follows:

$$B = \{B_1, B_2, ..., B_N\} \\ B_i = \{Tx_1,Tx_2, ..., Tx_m\}$$

In a sharded system, the blocks are uniquely divided into several subsets, with each subset corresponding to a specific shard, as follows: 

$$SB = \{SB_1, SB_2, ..., SB_k\}, \textrm{k -- number of shards} \\ SB_{i_j} \subset{B} \\ SB_i \cap SB_j = \{\emptyset\}, i \neq j$$

This demonstrates that each shard has its own designated transactions and designated blocks.

Therefore, we can define the global state of the sharded network as the combination of distinct, non-overlapping states of each shard:

$$S = S_1 \oplus S_2 \oplus... \oplus S_k; \oplus-\textrm{state merge function}\\ S_i \cap S_j = \{\emptyset\}$$

Similarly to how blocks are handled, we specify that the states of the shards are not explicitly shared. This simple concept provides an interesting property akin to sequential consistency.

$$S = f(G, SB_1) \oplus f(G, SB_2) \oplus ... \oplus f(G, SB_k) = f(G, B); \\\textrm{where G is genesis state, f -- state transition function}$$

This property holds because there are no concurrent modifications to the state of the same shard, meaning that the states can be computed independently and still lead to the same expected (deterministic) result.

Any system that operates in parallel must provide the ability to share data or state as a way of communication between units. This necessitates an interconnection between processing units, which, in our case, is referred to as cross-shard communication. To facilitate this, there is a special type of data sharing called a message that introduces changes to the state transition function and block space market:

$$S' = f(S, TX, MG), \textrm{where MG is a set of messages}, \\ B = \{TX, MG\}, \\ \forall{MG_i} \exists j, i\neq j|MG_i \cap MG_j \neq \{\emptyset\}, MG_i \subset SB_i, MG_j \subset SB_j$$

From the above, we see that the state transition function treats messages as a type of transaction. They are special because they modify some aspects of EVM execution, such as context recovery. For example, they use the source address instead of signature recovery without loss of security. However, from a consensus perspective, they are still considered ordinary transactions with similar properties. In a sharded system, each block includes such transactions, and more specifically, these messages are included in both the source and destination blocks. This is how inter-communication or state sharing is facilitated within the system.

We note that, based on the previously mentioned property, we can infer another property: transaction-level eventual consistency. This means that if a message is sent to multiple other shards (data sharing), all of them will eventually reach the latest state from the message. Simply, if we share some memory using a cross-shard message, as soon as it is emitted, every other shard will eventually observe its latest value from the message. Additionally, if transactions are reverted, the message is not emitted. They do this only when the source transaction is successfully validated.

In such a setup, messages cannot be lost because they are included in the source chain. Therefore, as long as data availability guarantees hold, if message i (i > j) is accessible, message j will also be accessible.

Rollups Sharding (main)

This section provides more detail on the proposal for the abstract sharded rollup.

Rollups operate on top of an L1 network to provide similar security guarantees while being faster and cheaper. To achieve this, modern rollups use the L1 network as settlement and data availability layers.

For the sharded rollup, the settlement layer is the main shard. It acts as a special "helper" network that is shared across all network participants (validators). Other shards verify their validity proofs on that network and store their latest state roots and DA commitment there. Additionally, the main shard functions as a synchronization point (ref. parallel systems) where shards can reach consistency. The settlement layer for the main shard is the L1 network. Therefore, we have the following setup:

$$S'_{main}=f(S_{main}, \{Tx_{root_1}, Tx_{root_2},..., Tx_{root_k}\} \cup\{Tx_{proof_1}, Tx_{proof_2},..., Tx_{proof_k}\})\\ S'_{L1} = f(S_{L1}, TX \cup\{Tx_{proof_{main}}\}), \textrm{f -- state transition function}$$

The only validity proof that needs to be verified on L1 is the state transition of the main shard. This, in turn, serves as a proof for the state transition of each individual execution shard. Hard finalization is achieved only when the validity proof of the main shard reaches finality on L1.

Although the sharded chain can be split into several non-intersecting sets, these sets cannot be processed independently. This is because the main shard's proof encompasses the state transition from time T to T+n (n≥1). During this period, each shard may produce a different number of blocks. Therefore, data availability commitment snapshots should be taken from the shards. These snapshots can consist of raw transactions or state diffs, but the specifics are not critical at this point.

While verifying the L1 data availability commitment of the main shard is relatively straightforward, especially with validity proof, which can be done, for example, through evaluation at a random point if it's a polynomial commitment, the challenge lies in proving the DA of other shards. This is where the state roots and block hashes on the main shard are used.

Simple proof

We can prove the equivalence of data from other shards by providing a Merkle proof of a shard's commitment within the main shard's state on the L1 chain contract. Since the commitment is part of the verified state of the main shard, this verification can be done cheaply and fast: $16log_{16}(N_i), N_i-\textrm{size of shard i trie}$. The proof is relatively small because the growth of the main shard's state is slow due to its specialized function. This straightforward approach allows other shards to cheaply and permissionlessly prove their DA commitments.

Parallel Execution and Efficiency

Understanding that rollup sharding is achievable and having established a basic description of it, we recognize how sharding aligns with the concept of parallel execution.

Preliminaries

We begin with a foundational but crucial observation. The Ethereum Virtual Machine (EVM) is a deterministic stack-based computational machine, and Solidity is a Turing-complete language. This setup allows for the implementation of an arbitrary set of algorithms (A). We have to mention it because, formally, a class of deterministic algorithms may not always be implemented on non-deterministic or memory-relaxed machines. For example, machines with weak oo-execution can’t support linear algebra computations. It’s also formally important to specify that Solidity is TC-language, as only in that case can you imply an arbitrary class of algorithms that we want to rely on.

However, not all algorithms from A can be efficiently parallelized, either theoretically or practically. It is well known that certain layout algorithms may resist parallelization. Our goal is to specify the class of algorithms that can theoretically be implemented efficiently in a sharded system.

Efficiency is defined as a function of three primary parameters: Gas, GasPrice(or Price), and work time T. W represents the workload of a single-chained solution, measured by the number of transactions processed.

GasPrice:* Parallelism can lead to increased gas expenditure due to the additional work for cross-shard communication. However, it can also result in significantly reduced gas prices (priority and moving average of base fee).

Work Time: Although parallelism might increase the latency associated with data exchange between shards, it significantly decreases the workload on each individual shard, potentially leading to faster processing times overall. We replace work time T as work divided by capacity (symbol C). So if we have an average of 100 TXs and C = 20, T = 5.

Let’s see a simple example (*we didn’t shorten the common parts intentionally for better visualization). Also, note that M is an approximation. The proof for the first statement will be presented later in the article. In this formula, M refers to the ratio of gas spent on messages against gas for transactions. So MG is gas associated with cross-shard communication (revealed later), which is overall transactions gas.

$$\\M \leftarrow MG/TX, |MG|\ll|TX|\\\\ W \textrm{-- workload, K -- number of shards(K>1), C -- capacity}\\ E_{price}: \theta(Gas \times Price)  > \Omega(Gas \times (1+O(M)) \times \theta(\frac{Price}{K}))\\(w.h.p.)E_{time} = \frac{W}{C} > \frac{W \times  (1 + O(M))}{K \times  C}$$

Let's first understand the concept of price inequality. The boundaries for a single-chain solution are relatively straightforward: the amount you pay is directly proportional to the amount of gas used and the price of that gas. For a sharded solution, we can assert that the lower bound will always be less than that of a single-chain solution.

To prove this, let's first compare the gas expenditure. In the case of a sharded solution, gas usage will increase due to the factor of cross-shard communication, meaning the gas cost will always be equal to or higher than that of a single-chain solution, since the factor cannot be less than 0.

The next part of the equation addresses the price function, which we assert grows strictly linearly with the number of shards. The intuition behind this is that linear growth is the only Pareto-optimal approach. From an economic perspective, fee models are likely to target this strategy to optimize for efficiency and fairness. However, real fee models may implement unfair strategies (we will not explore it in the modeling

The situation with work time is similar. If we define the capacity of a single chain as C, then the capacity for K shards would be K*C, adjusted for cross-shard communication. However, in this scenario, the inequality is much more strict. The only case where this might not hold true is if M approaches or exceeds K. Nonetheless, we assert this statement with high probability.

Proof of efficiency for cross-shard communication

With a critically high probability, M will never be 1 and, therefore, will not compete for block space as a source transaction. This stems from the idea that the expected gas cost for a transaction will almost always exceed the gas cost of a cross-shard transaction. Let's prove this by induction:

• In a classic single-chain VM, gas is used to cover memory and execution expenses. However, in the case of sharding, gas also needs to account for message transfers (as discussed in the section on rollups).
• Observation 0: calldata is the cheapest type of storage.
• Observation 1:

$$Gas_{sourceTX} = Gas_{message} + Gas_{data} + Gas_{execution}$$

• Observation 2: 

$$Gas_{message} < Gas_{sourceTX}$$

• Definition 1: 

$$\psi = \frac{Gas_{message}}{Gas_{store}+Gas_{execution}}$$

• Observation 3: if 

$$\forall TX:\psi < 1 \Rightarrow M < 1$$

• Observation 4: 

$$Gas_{message} = Gas_{calldata} + ^cGas_{construction} + ^cGas_{execution}$$

• Note: The construction and execution of cross-shard messages are constant and significantly smaller compared to even a simple transfer transaction. That’s because messages typically have fewer fields, and such things as signatures can be aggregated.
• Statement 1: if the source transaction is computationally intensive, the following is true: 

$$Gas_{message} \lll Gas_{execution} \Longrightarrow \psi \lll 1$$

• Proof: The cost of a cross-shard message doesn't depend on the execution of the transaction, as the opcode execution and message construction are constant and relatively small.
• Statement 2: if the transaction doesn’t produce message, the cost of it is 0: 

$$Gas_{message} = 0 \Longrightarrow \psi = 0$$

• Statement 3: if the transaction is memory intensive: the following is true: 

$$Gas_{message} < Gas_{data} \Longrightarrow \psi < 1$$

• Proof.
  • Case 1: In the case of transferring calldata only, if the contract execution involves operations on calldata of size X, the message will transfer data of size X', where X' ≤ X: $\psi \leq 1$.
  • Case 2: When transferring data from memory using a message, it will be less gas-consuming (def. 0) since messages transfer data as calldata. That means the following will always be true: 

$$Gas_{message(calldata)} < Gas_{data(memory)} \textrm{ as }|Message| \leq |Data|  \Longrightarrow \psi < 1$$

In this way, we've demonstrated that optimistically and with high probability, cross-shard messages will not introduce significant overhead compared to classic external calls, and considering the improvements from shards — the overall efficiency of such a system will dominate.

Parallel Applications

Let's consider a simple example of mapping a real application to a parallel task. We have a basic AMM DEX defined by two functions: u and d. d is the delta function, for example, xy=k. u is the state update function. An AMM is defined by the functions d and u where set of pools is $P = {P_1,...,P_n}$, and each is $P_i = \{a_{i_1}, a_{i_2}\}$, with a being an accumulator for some token. Note the following:

$$\forall P_i \cap P_j = \{\empty\}, i \neq j$$

That simple but crucial observation suggests that we can approach it by classifying parallel jobs:

$$Tasks = (d, u) \times P \\ Schedule = Tasks / K$$

That's it. We know that the update function u only takes two parameters: u(account, P_i). Since the states of the pools doesn't intersect, we can efficiently parallelize the AMM both in terms of time and cost. If the number of tasks exceeds the number of shards K, then by the pigeonhole principle, there will be at least two pools on the same shard. This is where the market is incentivized to support efficiency, so they will work on optimizing the scheduling of tasks, or in other words, in this case, pool distribution.

Conclusion

Observing concepts through the lens of a scientific discipline is a common approach to leveraging its properties and solutions. In this context, we have identified that sharding can be abstracted to Parallel Computation Theory, offering a new perspective on existing challenges. This abstraction allows us to inherit a wealth of studies, models, and algorithms, as demonstrated in this post.

Moreover, sharding is a technology that aligns with rollup design, introducing a novel environment that enhances scalability not only for the network but also for applications.

We have shown that parallel dApps represent the future of scaling the Web3 ecosystem. A parallel environment provides the opportunity to develop truly scalable applications that are more efficient than single-threaded approaches across all dimensions.

Parallelism is one of the most powerful tools for increasing the efficiency of systems and applications. Sharding makes parallelism possible.